This project was part of the 24-677 Linear Control Systems course at Carnegie Mellon. The primary objective was to develop a baseline Linear Quadratic Regulator (LQR) controller to fly an Unmanned Aerial Vehicle (UAV) without motor failure. The secondary objective was to design a Model-Reactive Adaptive Controller (MRAC) that would help stabilize the quadrotor if it lost more than half of thrust power in one of the rotors.
The project was designed solely in Webots—an open-source robotics simulation software—and performance of both controllers evaluated with plots and videos generated at the simulations’ conclusion. Both controllers were developed in Python.
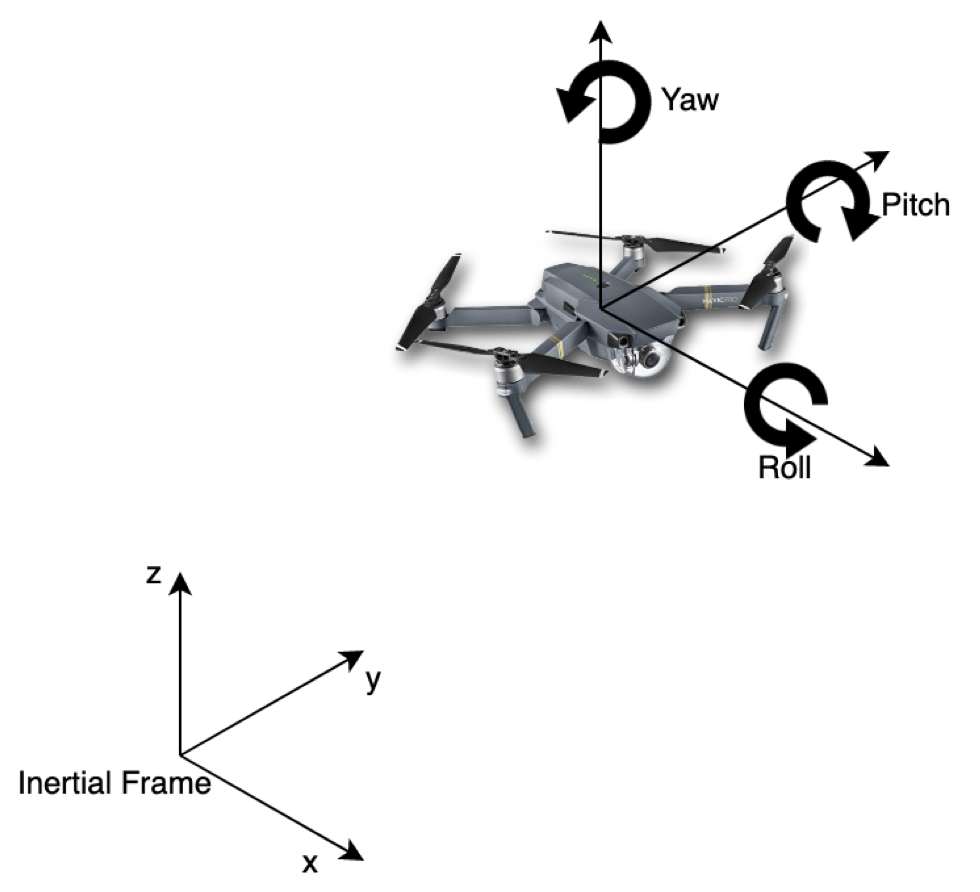
The quadrotor model used has the inertial frame fixed to the ground and the body frame is on the quadrotor in the cross-configuration where the +x-axis points forward w.r.t. to the body, in between motors 1 and 4 as shown in the figure below. The roll axis corresponds to rotation about the x-axis, pitch about the y-axis, and yaw about the z-axis.
Dynamics
The state of the system is described in position with x, y, z, and attitude with φ, θ, ψ, corresponding to roll, pitch, yaw. The system is linearized about the hover position where the inputs to the system are T, which is the collective thrust, and 𝛕_r, 𝛕_p, 𝛕_y which are the roll, pitch, yaw torques generated by the four propellers.
The state vector x_p is comprised of the position and attitude of the system, and their respective derivatives. The system is shown with the matrices A_p and B_p along with the state vector and the control input. The output of the system y_p is the state vector multiplied by the matrix C_p. These look like the following:
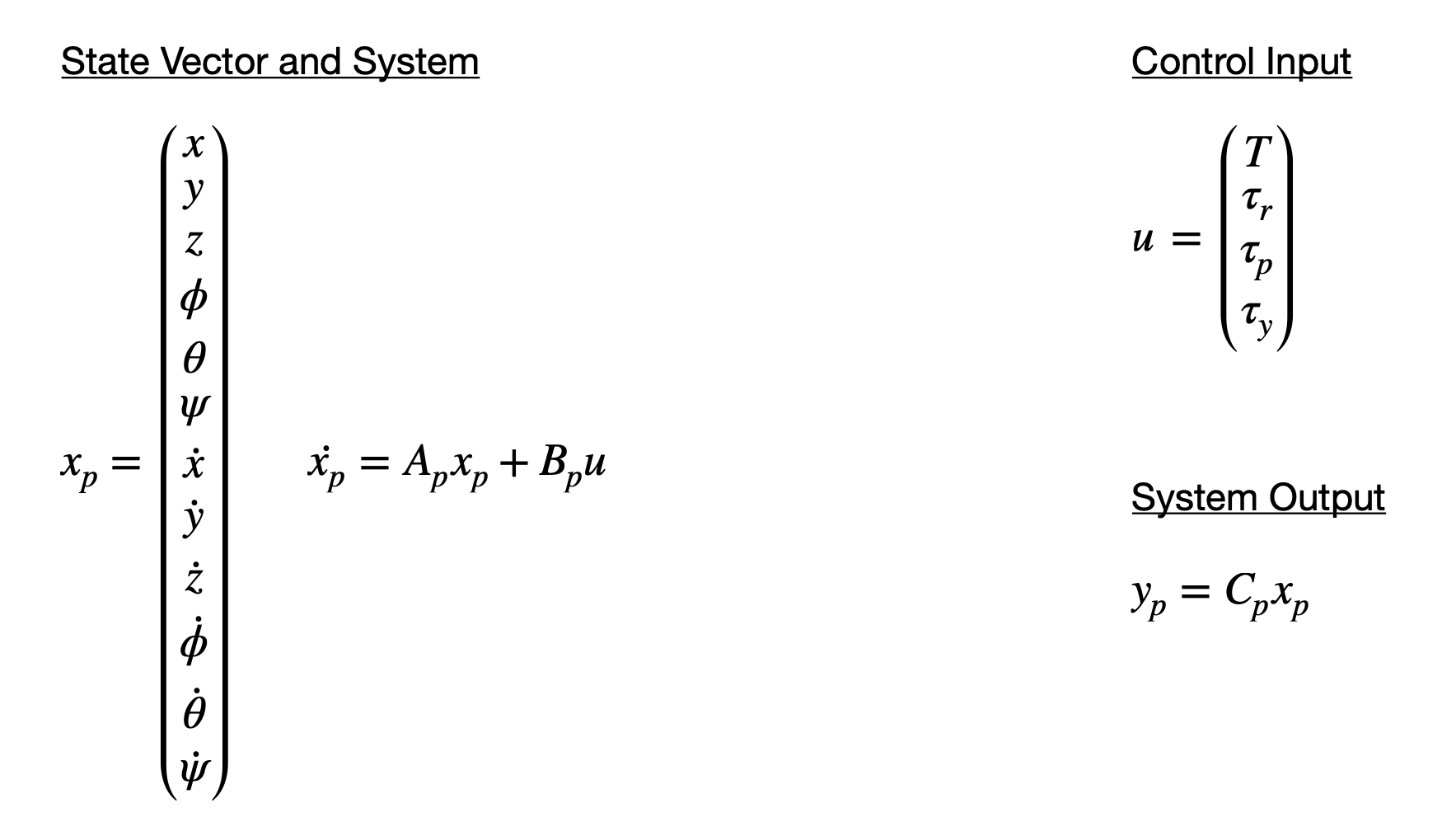
LQR
I designed a discrete-time infinite horizon LQR controller for the quadrotor to track a reference trajectory r when there is no motor failure. The reference trajectory changes along the z-axis where at different time intervals it indicates varying heights for the drone. Error between the current state and the desired state is defined as e_y and is taken to be the difference between the output y_p and the reference r, shown below.

The feedback gain matrix K is generated by adjusting the Q and R matrices directly. This feedback gain is then applied to the states x_p as shown below. In the case of tracking a reference trajectory as is the case for this project, x_p really becomes e_y.

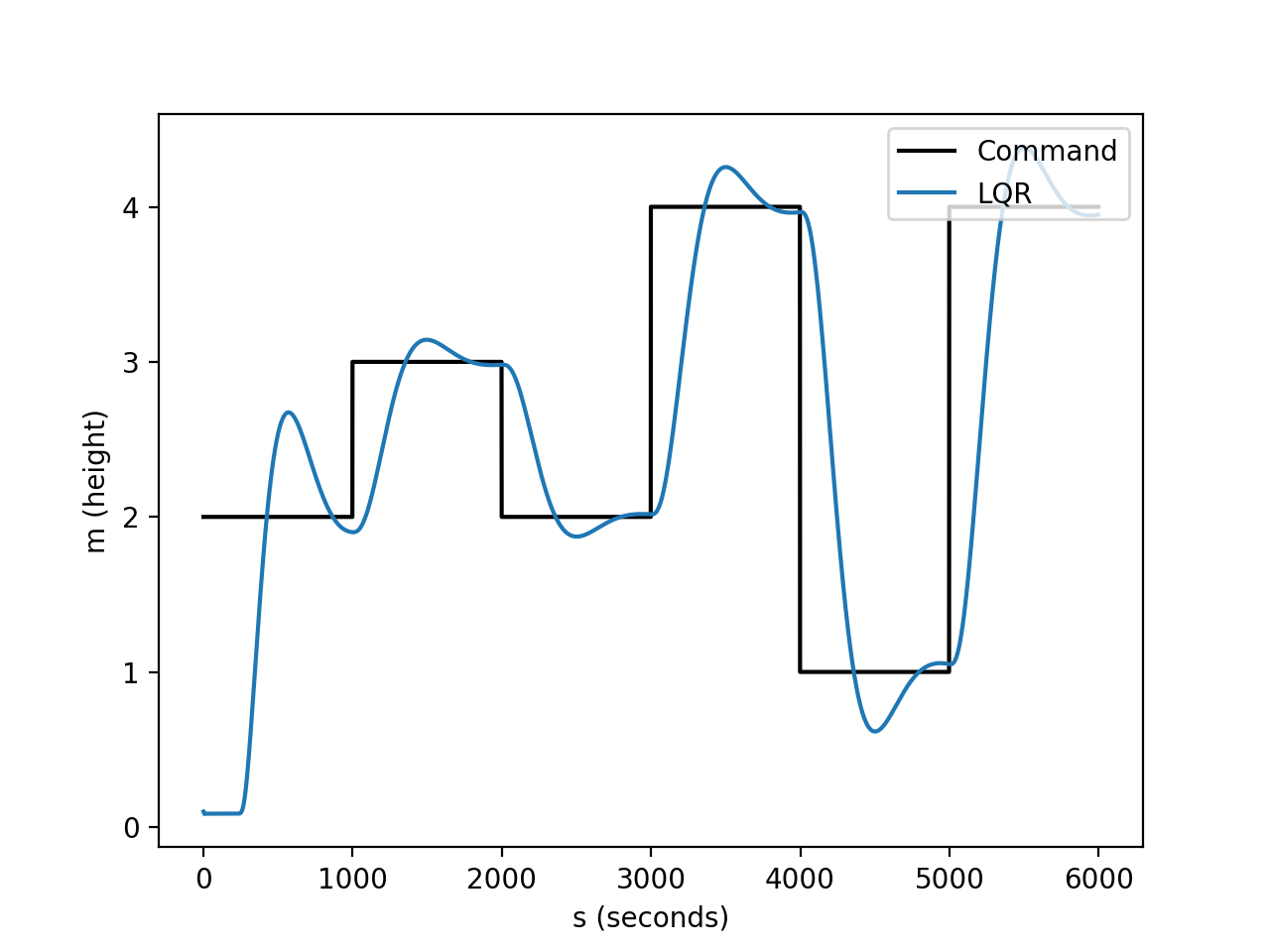
Performance of the LQR controller relative to the reference trajectory provided is shown in the plot below. It shows the reference trajectory (command) in the black line and the actual position of the drone along the z-axis in the blue line. The video on the left shows the simulation of the LQR controller tracking the reference trajectory with no motor failure introduced.
MRAC
To test out adaptive control theory, I implemented a MRAC and tested out its effectiveness in the event of a motor failure. During hovering, I analyzed how effective this algorithm is in maintaining hover in the event one of the motors loses 50% thrust and determine what the maximum allowable loss of thrust is before the controller fails.
Using the same system and setup as LQR and using LQR as the baseline controller, the MRAC is similar in that I generate the inputs using a gain matrix K_ad as seen in the equation below.
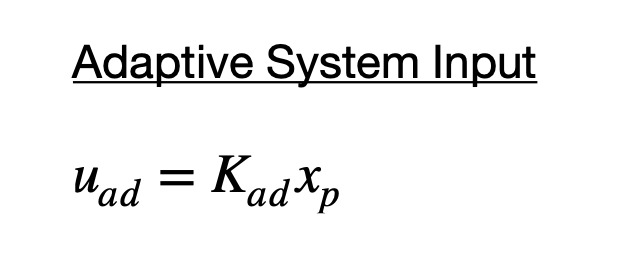
The augmented structure of the adaptive controller implies that in the nominal case, i.e. the case with no parameter uncertainty, the overall system is equivalent to the baseline controller. However in the case of a motor failure or when other uncertainties arise, the adaptive controller works to assist the baseline controller in maintaining stability and performance.
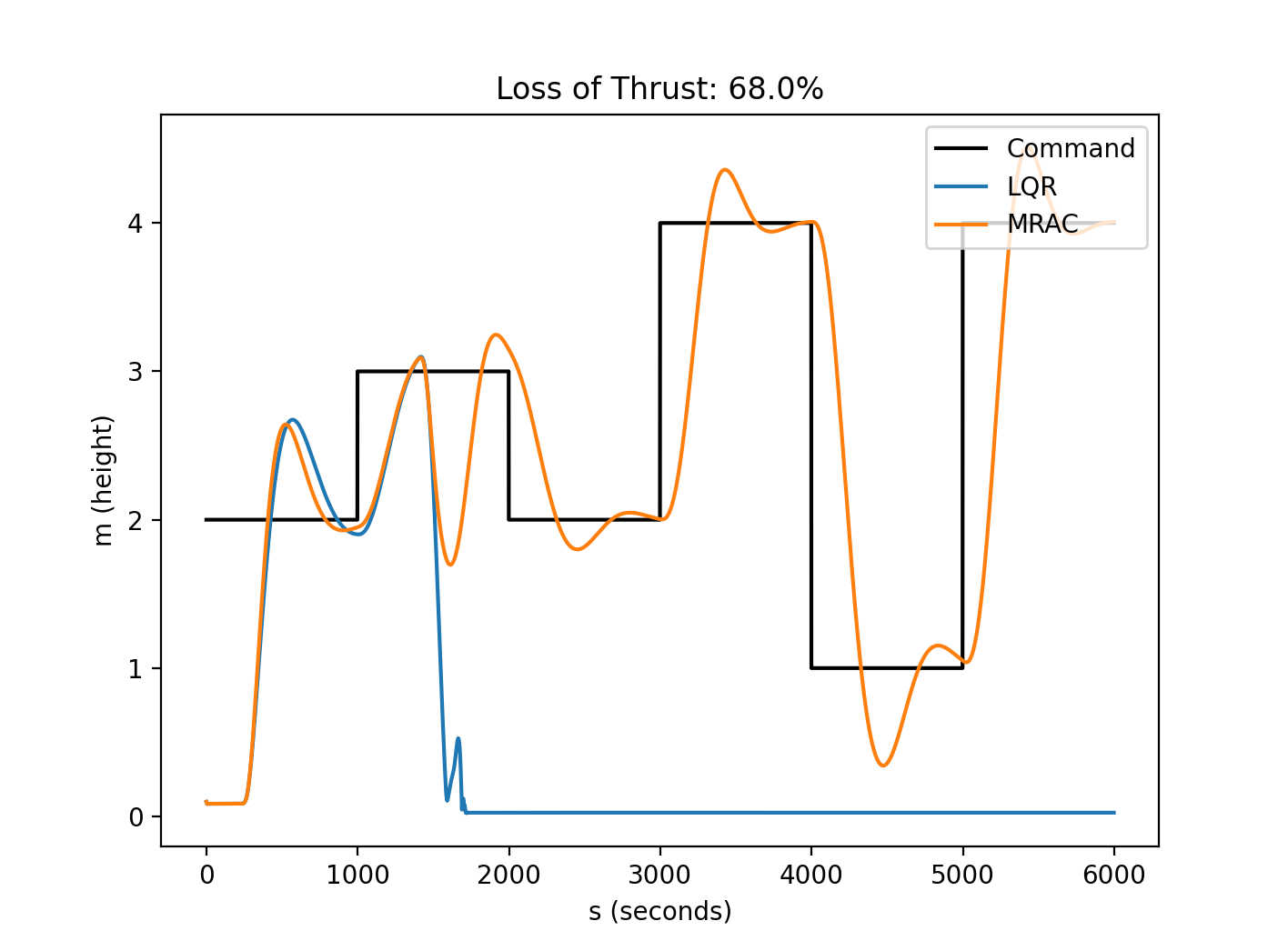
Through experimenting I determined the max loss of thrust the adaptive system can handle is 68%. In the plot below, performance of the baseline controller is shown in blue where that of the adaptive controller is shown in orange. Simulation for both controllers was ran at a loss of thrust of 68% and it’s clear that at ~1.5 sec, when the failure is introduced, the baseline controller fails to recover. However the adaptive controller performs well even with more than 50% loss of one of the motors. The video on the left shows the performance of the adaptive controller when the loss of thrust is introduced.